MCMC

New methods for Markov chain Monte Carlo sampling

Sampling from arbitrary distributions, that are usually not analytically available, can be a challenging but important task. For example in the context of Bayesian inference, drawing samples from the posterior is the go-to method to characterize this otherwise inaccessible distribution. Furthermore, calculating integral values of unnormalized distributions, for example the Bayesian “evidence” (i.e. marginal likelihood) is a key ingredient to model comparison.

In our paper “Integration with an Adaptive Harmonic Mean Algorithm” we introduce a technique that can reliably estimate integrals and uncertainties over a set of available samples, without any need to generate new samples.

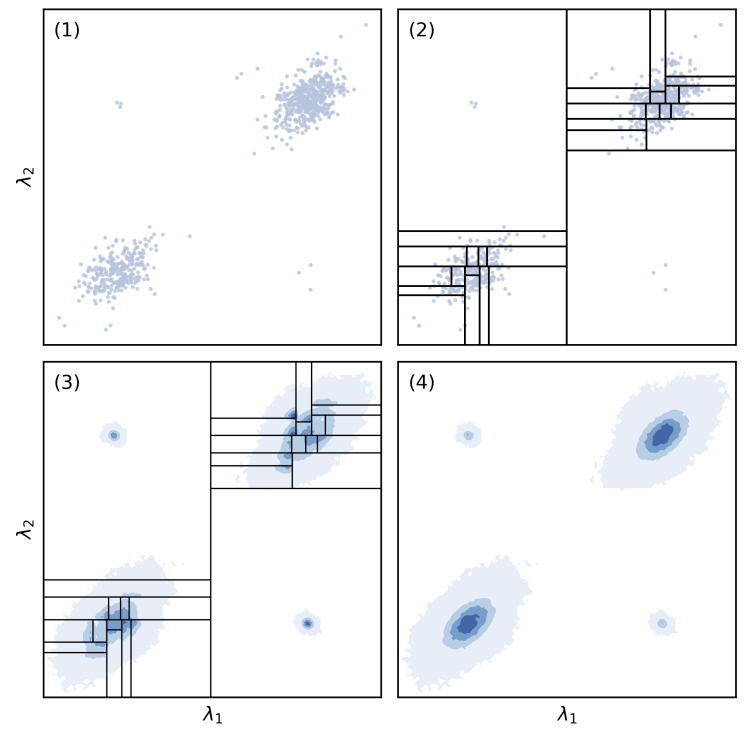
In our more recent work “Parallelizing MCMC Sampling via Space Partitioning” we use the above technique together with a space-partitioning scheme to parallelize the otherwise inherently serial Markov chain process. By doing so we can achieve super-linear scaling with the number of workers.

Illustration for the space partitioning algorithm sampling a multi-modal density. (1) initial exploration phase, (2) partitioning of the space, (3) sampling of individual sub-spaces, (4) re-weighting and stitching back together individual samples

Further Information

Collaborators: Prof. Dr. Allen Caldwell (MPP), Dr. Vasyl Hafytch (MPP), Dr. Oliver Schulz (MPP)

Paper on the adaptive harmonic integration: https://arxiv.org/abs/1808.08051

Paper on the parallel MCMC via space partitioning: https://arxiv.org/abs/2008.03098