spacings

Goodness-of-fit tests based on the spacings between ordered samples

Samples drawn from a uniform (left) and a non-uniform (right) distribution

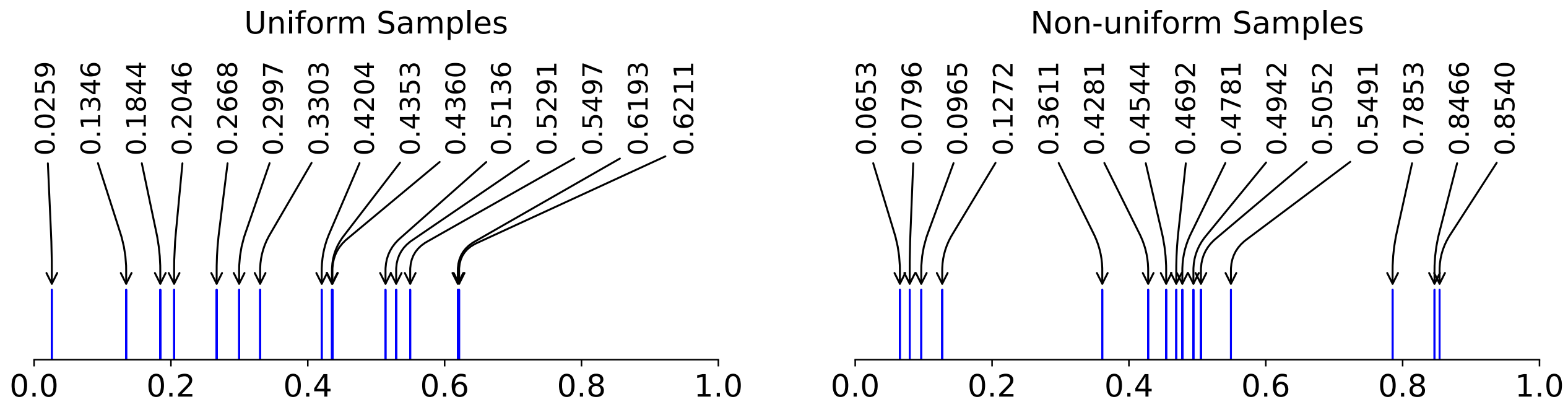
The figure above shows two examples of a set of samples drawn from a uniform and a non-uniform distribution, respectively. The aim here is to construct a sensitive test to decide if samples are compatible with the hypothesis of a uniform distribution.

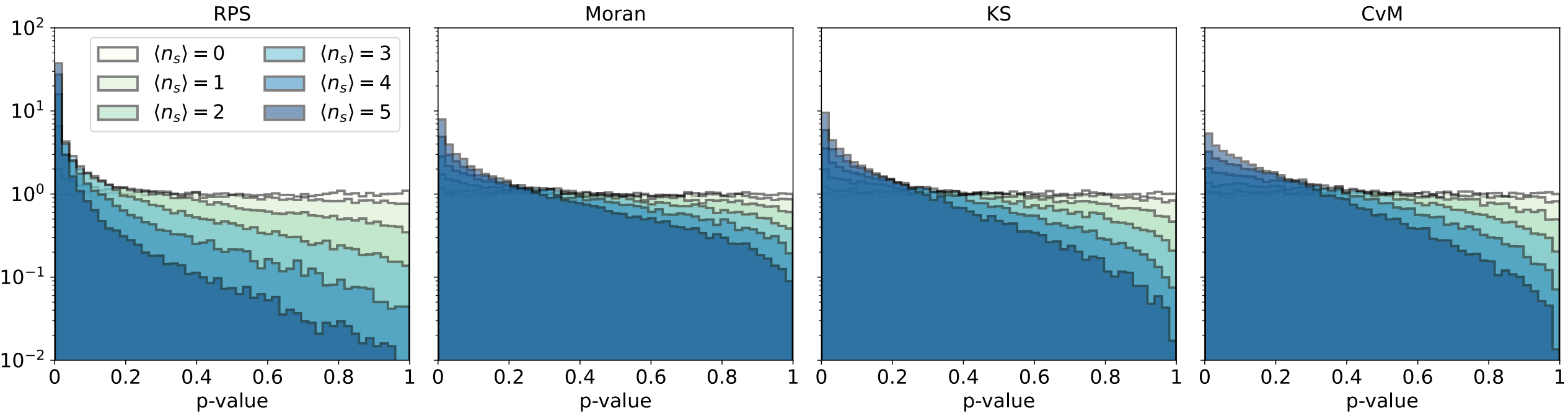
Some standard tests to assess this goodness-of-fit are, for example, the Kolmogorov-Smirnov, or the Anderson-Darling tests. In our work, we investigated test statistics based on the spacings between ordered samples, i.e. the distance between consecutive samples. Under a uniform distribution, the expectation value for such spacing is 1/n. If the samples are, however, drawn for example from a distribution featuring narrow “peaks”, we expect much smaller spacings. Our new test statistic “Recursive Product of Spacings” (RPS), can be very sensitive to such non-uniformities, and outperform other tests, as shown in the figure below.

Such tests find applications in many areas, ranging from the natural and social sciences over engineering to quality control.

Performance comparison of RPS (ours) vs. a few widely used test statistics. The p-value distributions pile up much more towards 0 for ns > 0 in the case of RPS, while the one for ns = 0 remains flat.

Further Information

Collaborators: Lolian Shtembari (MPP)

Preprint available: https://arxiv.org/abs/2111.02252

PyPI project page: https://pypi.org/project/spacings/